Evaluation of Tool Wear in Polymer Milling Process Using Non-Invasive Open-Source Monitoring System
DOI 10.5433/1679-0375.2024.v45.49800
Citation Semin., Ciênc. Exatas Tecnol. 2024, v. 45: e49800
Received: 6 February 2024 Received in revised for: 3 June 2024 Accepted: 1 July 2024 Available online: 7 August 2024
Abstract:
This study presents a non-invasive and affordable monitoring system to estimate the electrical current demand during the milling of acrylic and expanded PVC, with and without the use of cutting fluid. The proposed system consists of an Arduino® board integrated with an SCT-013-000 electrical current sensor, an RTC-DS3231 shield, and an SC Card shield, which perform the measurement and storage of the electrical current, values collected directly from the power cable of the Router Spindle TVS.1ZM3.12. Data were collected in a machinability test, where different concentrations of cutting fluid and cutting parameters (cutting speed and feed rate) were evaluated. Outputs included surface roughess, electrical current consumption, chip shape and tool wear. The results were statistically analyzed using analysis of variance (ANOVA), revealing that the different factors have individual effects on electrical current consumption. It was observed that tool wear contributed to an increase in the main motor’s consumption. Additionally, the reduction in electrical current consumption with the use of cutting fluid indicates a decrease in friction between the tool and the workpiece. space-0.4cm
Keywords: Arduino, cutting fluid, acrylic, PVC
Introduction
Machining of polymers by computer numerical control (CNC) still maintains several advantages compared to emerging layer-by-layer manufacturing technologies. However, some limitations, especially those related to intricate geometric details that cannot be easily milled, may pose challenges in tool production (Volpato & Amorim, 2011). As pointed out by Campos et al., 2015 and Gnatowski et al., 2023, engineering plastics are generally amenable to milling, cutting, drilling, grinding, and polishing operations, thus possessing the capability to undergo all common machining steps applied to metallic materials. Campos et al., 2015 further notes that machining tools used in plastic product manufacturing processes exhibit geometries comparable to those used in machining non-ferrous materials such as wood, as there have not yet been specific technological developments directed towards machining tools for plastic materials.
The monitoring of cutting tool condition is crucial in manufacturing systems and intelligent manufacturing (Prickett & Johns, 1999; Wang et al., 2021). Through a monitoring system, operators can obtain accurate information about the actual wear state of cutting tools, reducing the economic impacts resulting from potential tool breakage or the deterioration of product quality due to tool wear.
According to Prickett & Johns, 1999 and Hill et al., 2019, in indirect monitoring systems, the measurement of the target parameter is carried out through another parameter that can be measured in real-time and correlated with the former. Currently, this system has been receiving significant attention both academically and industrially, as unlike the direct method, it does not require interrupting the machining process, resulting in relative productivity gains. However, with indirect monitoring, wear ceases to be the sole monitored factor, being influenced by other variables such as cutting speed, machining depth, feed rate, as well as tool and workpiece materials.
For Kuntoğlu et al., 2021, measuring electrical parameters represents an indirect way of measuring cutting forces, as the machine tool’s motor generates the mechanical power required to perform a machining operation through the consumption of electrical current, which is directly proportional to the power and cutting forces.
Electrical current is a highly accurate indicator of cutting tool wear. Although fluctuations in power supply may occur during data collection, the associated errors are considered insignificant when compared to the range of application (Kuntoğlu et al., 2021).
The monitoring through electrical parameters of the motor presents several significant advantages (Reñones et al., 2010): it is a non-intrusive technique; it has low cost; its technology and operation are relatively simple; installation is easy; it does not require much space; it can be applied to most motors (AC and DC); it allows online process monitoring; and it is an effective system for milling operations, as power values are not very sensitive to tool entry shocks.
Low & Wong, 2011 investigated the polymer machining process and concluded that spindle speed, cutting speed, and feed rate are parameters that influence the surface integrity of the final workpiece. They observed that increasing spindle speed leads to a decrease in surface roughness, while increasing feed rate is associated with an increase in surface roughness.
Xiao & Zhang, 2002 analyzed the influence of tool feed rate and cutting speed on the temperature and finish of machined surfaces of polyamide and polyurethane thermoplastic polymers. The work revealed that viscous deformation, caused by temperatures in the cutting zone above the glass transition temperature of the polymers, played a decisive role in the surface finish quality of these materials. Furthermore, the best conditions noted were for high feed rates and low cutting speeds.
Thus, the objective of this work was to evaluate tool wear in the milling process of polymers using an open-source, non-invasive monitoring system.
Materials and methods
Material
This study investigated the effect of the electrical current consumed by the Spindle motor on the machinability of expanded PVC and acrylic polymers during the face milling process.
For the machining tests, a CNC Router Lexno equipped with a Spindle TVS.1ZM3.12 was used. The main specifications of the Spindle include a maximum speed of 18000 rpm and a nominal power of 1 HP. The cutting tool used in the process was a Rocast end mill with a cylindrical shank of 6 mm in HSS - 2 cuts.
The CNC programming of the process was conducted using the G-code language, with only one machining pass of 185 mm in length. At the end of each trial, the workpiece was removed for roughness measurement.
The cutting fluid used was MV AQUA 180, a water-based synthetic cutting fluid, transparent, non-toxic, and biodegradable, composed of organic raw materials that prevent the formation of solid residues on treated surfaces. According to the manufacturer, the recommended concentration of MV AQUA 180 typically ranges from 10 to 15 % (concentration, m/v), and it has a refractive index of 2.5.
The roughness gauge used to assess the average roughness of the test specimens was the RP-200 model from Instrutherm, with a measurement scale of 160 μm and an accuracy of less than 10 %. To measure the cutting fluid concentration, the analog refractometer Vodex VX090 from Vixshopping was used, with a scale from 0 to 90 % Brix.
The polymers used as specimens in the experiment were expanded PVC and acrylic in plate form with 200 mm × 200 mm × 10 mm.
For the acquisition system, we used the following components: Arduino Mega board, SCT-013-000 electrical current sensor, 120 Ω (5 %) resistor, 10 kΩ resistors for voltage division, 10 nF filter capacitor, jumpers, protoboard, DS3231 RTC module, and SD card module. The assembly configuration of the acquisition system can be seen in Figure 1.
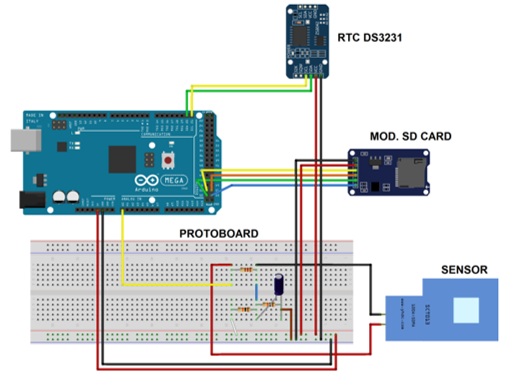
The SCT-013-000 sensor is capable of measuring a nominal electrical current of 100 A, producing output values between 0 and 50 mA proportional to the electrical current flowing in the main conductor. The logical programming of the Arduino and the other listed components was performed using the ARDUINO IDE software, and the measured data was stored on the SD Card module.
The construction of this data acquisition system required an investment of 350.00 Brazilian Reais. This makes it highly appealing compared to commercial acquisition systems. To validate the data collected by the acquisition system, we used an amperemeter clamp (Minipa).
Experimental design and data analysis
The cutting parameters selected in the pre-tests were defined to induce significant variations in the tool voltage, in order to provide a greater amplitude of electrical current detectable by the data acquisition system. To calibrate the system, the measured electrical current values were compared with those recorded by an amperemeter clamp.
For the tests, we opted for face milling to increase the voltage on the tool, consequently causing a greater variation in the measured electrical current. Machining operations were carried out on a CNC Spindle Router, both with and without the application of cutting fluid. The selected cutting parameters as input variables were cutting speed (vc) and feed rate (vf), while the depth of cut (ap) was kept constant at 0.5 mm in all situations.
Thus, two experiments were conducted at the Laboratory of the Group of Automation and Applied Instrumentation at the Federal Technological University of Paraná, Londrina Campus. The adopted experimental design was that of completely randomized blocks in a 23 factorial scheme, meaning two levels of cutting speed (vc), feed rate (vf), and material (PVC and acrylic), as illustrated in Table 1.
| Control Factors | Levels | Specifications |
|---|---|---|
| Cutting Speed (vc) | 2 | 150 – 250 [m/min] |
| Feed rate (vf) | 2 | 200 – 300 [mm/min] |
| Material | 2 | PVC – Acrylic |
So, in the first experiment we have:
Six blocks: three blocks without cutting fluid (B1, B2 and B3) and three blocks with cutting fluid (B4, B5 and B6);
In each block, eight treatments (combinations of factor levels) were randomized, totaling 48 trials;
For each trial, the response variable observed was the electrical current.
In the second experiment we have:
Twelve blocks: three blocks without cutting fluid (B1, B2, and B3), three blocks with low concentration (5 %) of cutting fluid (B4, B5, and B6), three blocks with ideal concentration (12 %) of cutting fluid (B7, B8, and B9), and three blocks with high concentration (27.50 %) of cutting fluid (B10, B11, and B12).
In each block, eight treatments were randomized again, totaling 96 trials.
For each trial, the response variables observed included roughness, chip sample and electrical current variation. The average roughness (Ra) values were collected in the machined range and always adopting the direction of the cutting tool feed.
For the cutting fluid analysis, samples were collected, verifying the pH and conductivity behavior.
The cutting fluids, in the experiment, were prepared by adding the product concentrate to the mixture in the milling machine reservoir. The concentration of the mixture was measured with a refractometer, obtaining the value in degrees Brix, multiplying the result by the refractive index factor provided by the manufacturer. The tests consisted of a single pass through the linear milling operation, performed on the flat surface of two polymers, applying three different concentrations of the cutting fluid.
In this context, statistical analysis of the data was performed. Thus, considering a significance level of 5 %, the following hypotheses were tested in the analysis of variance (ANOVA):
H0: There is no block (cutting fluid) effect versus H1: There is block (cutting fluid) effect.
H0: There is no triple interaction effect versus H1: There is triple interaction effect.
H0: There is no double interaction effect versus H1: There is double interaction effect.
On the other hand, if the null hypothesis is rejected in both cases, the following hypotheses will be tested:
H0: There is no effect of cutting speed versus H1: There is an effect of cutting speed.
H0: There is no effect of feed rate versus H1: There is an effect of feed rate.
H0: There is no material effect versus H1: There is a material effect.
The procedure for obtaining the test statistic (F0) and its respective descriptive level are summarized in an ANOVA table for a completely randomized block design, as demonstrated in Montgomery, 2013. In cases where the effects of the controlled factors are significant, a Tukey’s Mean Comparison Test is conducted to test the following statistical hypotheses: H0: There is no difference between the means versus H1: There is at least one pair of means that are different from each other.
Results and discussion
Preliminary tests with no-load machining were conducted to verify the accuracy of the data acquisition system, obtaining reference values for the electrical current consumption of the CNC Spindle motor during no-load movement. After this procedure, the tests were performed in the defined order, and the interaction of the variable levels with respect to the electrical current consumed by the Spindle motor was analyzed.
Initially, a residue analysis was conducted considering all response variables. The results of the Shapiro-Wilk test did not indicate rejection of the hypothesis of residue normality (p-value >0.05). With the assumptions met, the ANOVA was performed.
ANOVA of the electrical current data
A summary of the ANOVA results is provided in Table 2. These results indicate that the null hypothesis (H0) defined in the Experimental Design regarding the triple interaction was not rejected (p-value >0.05). Therefore, there was no effect of the triple interaction on the electrical current. The same observation applies to double interactions; none of them showed a significant interaction effect (p-value >0.05).
| Source of Variation | Degrees of Freedom | Sum of Squares | Mean Square | F0 | p-value |
|---|---|---|---|---|---|
| Block | 5 | 0.48562 | 0.00971 | 153.42 | 0.000 |
| vc | 1 | 0.01587 | 0.01587 | 250.69 | 0.000 |
| vf | 1 | 0.00054 | 0.00054 | 8.49 | 0.006 |
| Material | 1 | 0.00130 | 0.00130 | 20.6 | 0.000 |
| vc:vf | 1 | 0.00012 | 0.00012 | 1.87 | 0.180 |
| vc : Material | 1 | 0.00001 | 0.00001 | 0.87 | 0.357 |
| vf : Material | 1 | 0.00001 | 0.00001 | 0.16 | 0.692 |
| vc:vf : Material | 1 | 0.00003 | 0.00003 | 0.51 | 0.482 |
| Residuals | 35 | 0.00221 | 0.00006 | – | – |
| Total | 47 | 0.68705 | – | – | – |
As discussed in the Experimental Design, if the interaction effects are not significant, the main effects are evaluated. As evidenced by the data in Table 2, all main effects are statistically significant (p-value < 0.05). Therefore, we have evidence that there is an effect of blocks, cutting speed, feed rate, and material. Figure 2 illustrates the dispersion of the mean electrical current according to the factors under study, visually demonstrating the interaction effects, which corroborates the results of the Analysis of Variance.
![fig: Behavior of the parameters with effect on the electrical current [A].](https://ojs.uel.br/revistas/uel/index.php/semexatas/article/download/49800/version/68837/50845/278220/Figure_2.png)
The results of the Tukey’s Mean Comparison Test are presented in Table 3. The blocks corresponding to the tests without cutting fluid show higher electrical current consumption, with their mean values differentiated only into two groups, A and B. Meanwhile, the blocks corresponding to the tests with cutting fluid, each block was differentiated into groups C, D, and E, indicating a gradual increase in the average electrical current with each block. This behavior is possibly due to tool wear, as evidenced in Figure 4.
| Block | Mean Current [A] | Group |
|---|---|---|
| B1 | 1.80416 | A |
| B2 | 1.79680 | A and B |
| B3 | 1.79198 | B |
| B4 | 1.72288 | E |
| B5 | 1.73611 | D |
| B6 | 1.75038 | C |
| (a) | (b) |
 |  |
When analyzing Table 4, it becomes evident that the electrical current consumption increases both with the increase in cutting speed and feed rate. In both cases, there is a statistically significant difference at a significance level of 5 % in the mean comparison test conducted by the Tukey method. These findings are consistent with those of Patra et al., 2007. Regarding materials, there is variation in the demand for electrical current among the analyzed polymers, with higher electrical current consumption during milling of acrylic.
| Cutting Speed [m/min] | Mean Current [A] | Group | |
| 250 | 1.7852 | A | |
| 150 | 1.7488 | B | |
| Feed Rate [mm/min] | Mean Current [A] | Group | |
| 300 | 1.7704 | A | |
| 200 | 1.7637 | B | |
| Mean Current [A] | Group | ||
| Acrylic | 1.7704 | A | |
| PVC | 1.7637 | B |
ANOVA of the influence of the cutting fluid concentration xxxxxxxxxxxxxxxxx
In the second test, the average roughness was measured at three points, beginning, middle and end of machining and the ANOVA of the roughness data is summarized in Table 5. It is noted that there was no effect of triple interaction and the interactions between vc and vf and the interactions between vf and material (p-value >0.05). However, the H0 about non-effect of the interaction between material and cutting speed on the average roughness data was rejected (p-value <0.05). The same is observed for blocks (p-value<0.05).
After finding the factors that affect the roughness data, we proceed to perform the respective Tukey’s Mean Comparison Tests: between the interaction and effect of the block. For the interaction between cutting speed and material, Table 6 shows that in machining with PVC, the lower speed had a greater effect on the average roughness. Whereas in acrylic, at higher speeds, the average roughness increased. This fact is linked to the increased friction caused by the higher cutting speed, along with the greater difficulty of heat dissipation in this material.
| Source of Variation | Degrees of Freedom | Sum of Squares | Mean Square | F0 | p-value |
|---|---|---|---|---|---|
| Block | 11 | 41.412 | 3.765 | 4.580 | 0.000 |
| vc | 1 | 2.196 | 2.196 | 2.670 | 0.106 |
| vf | 1 | 0.083 | 0.083 | 0.100 | 0.751 |
| Material | 1 | 155.110 | 155.110 | 188.500 | 0.000 |
| vc:vf | 1 | 0.172 | 0.172 | 0.210 | 0.649 |
| vc : Material | 1 | 46.567 | 46.567 | 56.590 | 0.000 |
| vf : Material | 1 | 0.038 | 0.038 | 0.050 | 0.830 |
| vc:vf : Material | 1 | 0.001 | 0.001 | 0.000 | 0.971 |
| Residuals | 77 | 63.360 | 0.823 | – | – |
| Total | 95 | 308.938 | – | – | – |
| Material | Cutting Speed [m/min] | Mean | Group |
|---|---|---|---|
| 150 | 5.21321 | A | |
| 250 | 4.12275 | B | |
| 250 | 2.97346 | A | |
| 150 | 1.27804 | B |
Using the Tukey Average Comparison Test with a block effect on the average roughness, it may be observed that roughness increases in the absence of cutting fluid during the experiment. Additionally, blocks B1 and B2 showed lower values compared to block B3. The same behavior is noted in the other treatments. With little fluid, B4 presents lower values and is different from B5 and B6. In treatment with the ideal volume of fluid, B7 presents lower values and is different from B8 and B9. And with fluid volume above the ideal, B10 and B11 have lower values and different from B12. These facts indicate that tool/material friction decreases with increasing cutting fluid concentration and that the tool wears out over the course of its use, even with the presence of the fluid.
| Block | Mean | Group |
|---|---|---|
| B6 | 4.6265 | A |
| B3 | 4.5996 | A |
| B2 | 3.6595 | A and B |
| B5 | 3.4461 | A and B |
| B8 | 3.4211 | A and B |
| B1 | 3.3730 | A and B |
| B12 | 3.3624 | A and B |
| B9 | 3.3529 | A and B |
| B7 | 3.0381 | B |
| B4 | 2.9740 | B |
| B11 | 2.6260 | B |
| B10 | 2.2831 | B |
ANOVA of roughness at the machining midpoint xxxxxxxxxxxxxxxxxxxxxxxxxx
The ANOVA of the roughness at the machining midpoint data is summarized in Table 8. It is noted that there was no triple and double interaction effect between vc and vf and vf and material, because the H0, defined in Experimental Design, was not rejected (p-value <0.05). On the other hand, there is an interaction effect between material and cutting speed (p-value <0.05) on the average roughness data and also, there is a block effect (p-value <0.05).
| Source of Variation | Degrees of Freedom | Sum of Squares | Mean Square | F0 | p-value |
|---|---|---|---|---|---|
| Block | 11 | 26.475 | 2.407 | 2.330 | 0.016 |
| vc | 1 | 0.203 | 0.203 | 0.200 | 0.659 |
| vf | 1 | 0.210 | 0.210 | 0.200 | 0.653 |
| Material | 1 | 202.455 | 202.455 | 196.160 | 0.000 |
| vc:vf | 1 | 0.129 | 0.129 | 0.130 | 0.724 |
| vc : Material | 1 | 55.913 | 55.913 | 54.170 | 0.000 |
| vf : Material | 1 | 0.136 | 0.136 | 0.130 | 0.718 |
| vc:vf : Material | 1 | 0.043 | 0.043 | 0.040 | 0.839 |
| Residuals | 77 | 79.471 | 1.032 | – | – |
| Total | 95 | 365.034 | – | – | – |
After finding the factors affecting the roughness data, we proceed to perform the respective Tukey’s Mean Comparison Test: between the interaction and the block effect.
Tukey’s mean comparison test – double interaction between cutting speed and material: midpoint machining roughness
PVC exhibits higher roughness values than Acrylic, as seen in Table 9. In terms of midpoint machining roughness, it is observed that a cutting speed of 150 m/min results in a different and higher roughness compared to 250 m/min for PVC. Conversely, for Acrylic, a cutting speed of 150 m/min yields lower roughness than that observed with a speed of 250 m/min, which is attributed to Acrylic’s greater difficulty in dissipating heat generated by increased friction at higher speeds.
| Material | Cutting Speed [m/min] | Mean | Group |
|---|---|---|---|
| 150 | 5.72938 | A | |
| 250 | 4.29496 | B | |
| 250 | 2.91688 | A | |
| 150 | 1.29863 | B |
Tukey’s mean comparison test – block effect on average roughness xxxxxxxx
Table 10 shows that, in the absence of cutting fluid (B2 and B3) and with low concentrations of cutting fluid (B6 and B5), the average roughness values were higher. This suggests that cutting fluid generally has an impact on the machinability of the polymers. However, at the beginning of tool use (B1 and B4), when the tools are still sharp, the roughness values were lower. On the other hand, for high concentrations (B10 and B11) and with the cutting fluid at the ideal concentration (B7 and B8), the average roughness values were lower, demonstrating that the friction between the tool and the material decreases with the increase of the cutting fluid concentration. Yet, even with the cutting fluid (B9 and B12), with greater use of the cutting tool, a small increase in roughness is observed.
| Block | Mean | Group |
|---|---|---|
| B3 | 4.7428 | A |
| B12 | 3.8920 | A and B |
| B2 | 3.8666 | A and B |
| B5 | 3.8363 | A and B |
| B9 | 3.8290 | A and B |
| B6 | 3.7366 | A and B |
| B1 | 3.4409 | A and B |
| B8 | 3.3443 | A and B |
| B11 | 3.2488 | A and B |
| B7 | 3.1201 | A and B |
| B4 | 3.0685 | A and B |
| B10 | 2.5938 | B |
ANOVA of roughness at the machining endpoint xxxxxxxxxxxxxxxxxxxxxxxxxx
The ANOVA of the roughness at the machining end point data is summarized in Table 11. Through analysis, it is noted that there was no effect of triple interaction as well, as well as the interaction between vc and vf and vf and material (p-value >0.05). Although, the H0 about non-effect of the interaction between material and cutting speed on the average roughness data was rejected (p-value <0.05). The same is observed for blocks (p-value <0.05).
| Source of Variation | Degrees of Freedom | Sum of Squares | Mean Square | F0 | p-value |
|---|---|---|---|---|---|
| Block | 11 | 30.189 | 2.744 | 2.430 | 0.012 |
| vc | 1 | 4.039 | 4.039 | 3.570 | 0.063 |
| vf | 1 | 0.106 | 0.106 | 0.090 | 0.760 |
| Material | 1 | 182.367 | 182.367 | 161.240 | 0.000 |
| vc:vf | 1 | 0.122 | 0.122 | 0.110 | 0.743 |
| vc : Material | 1 | 45.033 | 45.033 | 39.820 | 0.000 |
| vf : Material | 1 | 0.020 | 0.020 | 0.020 | 0.894 |
| vc:vf : Material | 1 | 0.156 | 0.156 | 0.140 | 0.712 |
| Residuals | 77 | 87.087 | 1.131 | – | – |
| Total | 95 | 349.119 | – | – | – |
After finding the factors affecting the roughness data, we proceed to perform the respective Tukey’s Mean Comparison Tests: between the interaction and the individual effects.
Tukey’s mean comparison test – double interaction between cutting speed and material: endpoint machining roughness
Table 12 shows that PVC has higher roughness values compared to acrylic at the end point of measurement, as previously observed in the midpoint analysis (Table 9, maintaining a consistent trend regardless of the machining stage. For PVC, a cutting speed of 150 m/min results in a roughness that is different and higher than at a speed of 250 m/min. Conversely, for acrylic, a cutting speed of 150 m/min results in a roughness that is different and lower compared to 250 m/min. This behavior is related to the difficulty of acrylic in dissipating the heat generated by the increased friction due to the higher cutting speed.
| Material | Cutting Speed [m/min] | Mean | Group |
|---|---|---|---|
| 150 | 5.32921 | A | |
| 250 | 4.36963 | B | |
| 250 | 2.98287 | A | |
| 150 | 1.20283 | B |
Tukey’s mean comparison test – block effect on average roughness xxxxxxxx
Table 13 shows that in the absence of cutting fluid (B2 and B3) and with low concentration cutting fluid (B5 and B6), the average roughness values were higher. This indicates that the cutting fluid influences the machinability of the materials, particularly at the beginning of the machining process. On the other hand, for high concentrations (B10) and with cutting fluid at the ideal concentration (B7 and B8), the average roughness values were lower, demonstrating that the friction between the tool and the material decreases with increasing fluid concentration. cutting. An outlier is observed in treatments B1 and B4, which in the absence of cutting fluid presents low roughness, statistically differing from the other treatments without cutting fluid. This result was influenced by the initial sharpening condition of the tool, as it was in its first use. Tables 7 and 10 also show a tendency for treatments B1 and B4 to present lower roughness than the other treatments; however, statistically, they are equal at the 5 % significance level. Treatments B9, B11 and B12 showed a slight increase in roughness even with higher fluid concentrations.
| Block | Mean | Group |
|---|---|---|
| B3 | 4.7765 | A |
| B9 | 3.9519 | A and B |
| B6 | 3.7661 | A and B |
| B2 | 3.7304 | A and B |
| B5 | 3.7028 | A and B |
| B11 | 3.5841 | A and B |
| B12 | 3.3866 | A and B |
| B8 | 3.3728 | A and B |
| B1 | 2.9751 | B |
| B4 | 2.8953 | B |
| B10 | 2.7746 | B |
| B7 | 2.7375 | B |
Chip Analysis
As machining progressed, the formation of chip types was observed in both polymers, varying only in size. In the case of PVC, during dry machining and with low and ideal concentrations of cutting fluid, a significant amount of burrs was formed during the process, while machining with high concentration resulted not only in small chip flakes but also in helical chips of the short washer type, instead of prominent burrs. Additionally, there was a decrease in chip size with increasing cutting fluid concentration, which is related, according to Yan et al., 2022, to the decrease in material ductility. In the case of acrylic, during dry machining, the chips became more opaque, while with increasing cutting fluid concentration, the chips decreased in size, as expected.
Cutting fluid analysis
During all trials containing the cutting fluid, conductivity and pH data were collected to monitor its behavior. The pH remained practically unchanged among the low (9.1), ideal (9.1), and high (9.2) concentrations of the cutting fluid. Conversely, conductivity increased in value according to the concentration variation: low (3.61), ideal (6.47), and high (8.93) cutting fluid concentrations.
Another important factor observed was that as the cutting fluid concentration increased, its odor became stronger, requiring the use of masks to avoid affecting human health, as mentioned by Sales et al., 2001. Additionally, the cutting fluid became increasingly viscous at higher concentrations. It is also important to note, corroborating Valentim et al., 2023, that the temperature variation caused by the cutting fluid can interfere with the machining process outcome.
Tool cooling was also noticeable with the application of cutting fluid in the machining process of polymeric materials. At high concentrations of the cutting fluid, in addition to the strong odor, the expanded PVC parts showed slight darkening and light stains, even after cleaning the part with water after the machining process, a fact not noticed in other concentrations.
Conclusions
After analyzing the experimental data to assess the influence of control parameters on electrical current variation, it was observed that all parameters individually affected the electrical current. However, cutting speed emerged as the most significant factor in motor electrical current consumption, while feed rate and material type showed less impact.
The electrical current recorded in the test blocks with cutting fluid was lower than that observed in dry tests. Additionally, the results revealed a gradual increase in average electrical current with each repetition of tests using cutting fluid, indicating progressive tool wear. Consequently, tool wear also influences the monitored electrical current value.
Through analysis of variance, it was observed that the interaction between cutting speed and material had a significant influence on average roughness data. This was evident with higher values when machined at 150 m/min in PVC and at 250 m/min in acrylic. In terms of materials, the machining process in acrylic demonstrated superior surface quality compared to expanded PVC, reflected in lower average roughness values. As for feed rate, its variation did not show a significant effect on surface integrity.
Furthermore, analysis of variance confirmed that the cutting fluid influences the surface integrity of the workpieces, as average roughness values decreased as the concentration of MV Aqua 180 cutting fluid increased.
Finally, the collection and storage of electrical current data, carried out using an open-source system, demonstrated sensitivity to non-invasively analyze the milling process behavior.
Author contributions
R. B. Michels participated in: Conceptualization, Methodology, Programs, Resources, Writing – revision and editing. J. F. S. Gonçalves participated in: Conceptualization, Methodology, Projects Managements, Resources, Supervision – Writing – original draft. M. F. Gimenez participated in: Data Curation, Investigation, Resources, Validation, Visualization, Writing – original draft. R. T. Boa Sorte participated in: Data Curation, Investigation, Resources, Validation, Visualization, Writing – original draft. E. M. Hashimoto participated in: Formal Analysis, Methodology, Validation, Writing – revision and editing.
Conflicts of interest
The authors certify that no commercial or associative interest represents a conflict of interest concerning the manuscript.
References
Campos, J. C. R., Panzera, T. H. & Scarpa, F. (2015). Machining behaviour of three high-performance engineering plastics. 229(1), 28--37. https://doi.org/10.1177/0954405414525142
Gnatowski, A., Golebski, R., Sikora, P., Petru, J. & Hajnys, J. (2023). Analysis of the impact of changes in thermomechanical properties of annealed semi-crystalline plastic on the surface condition after the machining process. 16(13), 1--16. https://doi.org/10.3390/ma16134816
Hill, J. L., Prickett, P. W., Grosvenor, R. I. & Hankins, G. (2019). The practical exploitation of machine tool intelligence. 1693--1707. https://doi.org/10.1007/s00170-019-03963-0
Kuntoğlu, M., Aslan, A., Pimenov, D. Y., Usca, Ü. A., Salur, E., Gupta, M. K., Mikolajczyk, T., Giasin, K., Kaplonek, W. & Sharma, S. (2021). A review of indirect tool condition monitoring systems and decision-making methods in turning: Critical analysis and trends. 21(1), 1--32. https://doi.org/10.3390/s21010108
Low, K. O. & Wong, K. J. (2011). Influence of ball burnishing on surface quality and tribological characteristics of polymers under dry sliding conditions. 44(2), 144--153. https://doi.org/10.1016/j.triboint.2010.10.005
Montgomery, D. C. (2013). Design and Analysis of Experiments. John Wiley \& Sons.
Patra, K., Pal, S. K. & Bhattacharyya, K. (2007). Artificial neural network based prediction of drill flank wear from motor current signals. 7(3), 929--935. https://doi.org/10.1016/j.asoc.2006.06.001
Prickett, P. W. & Johns, C. (1999). An overview of approaches to end milling tool monitoring. 39(1), 105--122. https://doi.org/10.1016/S0890-6955(98)00020-0
Reñones, A., Rodríguez, J. & Miguel, L. J. de (2010). Industrial application of a multitooth tool breakage detection system using spindle motor electrical power consumption. 517--528. https://doi.org/10.1007/s00170-009-2119-3
Sales, W. F., Diniz, A. E. & Machado, Á. R. (2001). Application of cutting fluids in machining processes. 23(2), https://doi.org/10.1590/S0100-73862001000200009
Valentim, M. de M., Santos, A. L. dos, Sichieri, V. J. & Gonçalves, J. F. de S. (2023). {Evaluation of Intergranular Corrosion in 7050-T7451 Aluminum Structures Influenced by Temperature and Contact with Cutting Fluid. 47981. https://doi.org/10.5433/1679-0375.2023.v44.47981
Wang, Q., Wang, H., Hou, L. & Ui, S. (2021). Overview of tool wear monitoring methods based on convolutional neural network. 11(24), 12041. https://doi.org/10.3390/app112412041
Xiao, K. Q. & Zhang, L. C. (2002). The role of viscous deformation in the machining of polymers. 44(11), 2317--2336. https://doi.org/10.1016/S0020-7403(02)00178-9
Yan, P., Wang, Y., Jin, X., Zhu, J., Jiao, L., Qiu, T. & Wang, X. (2022). Effect of cutting fluid on high strain rate dynamic mechanical property and cutting performance of nickel based superalloy. 1146--1158. https://doi.org/10.1016/j.jmrt.2022.01.080
Volpato, N. & Amorim, J. R. de (2011). A procedure for dealing with milling limitations in machined prototype tooling. 225(12), 2163--2176. https://doi.org/10.1177/0954405411404478

