Shear Strength of Hybrid Fiber Reinforced Self-Compacting Concrete Beams
da Silva, I. E.; Laufer, I. G.; Savaris, G.; Mendoza-Fakhye, R. J.; Balestra, C. E. T.; Bergmann, A. C
DOI 10.5433/1679-0375.2023.v44.48549
Citation Semin., Ciênc. Exatas Tecnol., v. 44: e48549
Abstract:
Self-compacting concrete has constructive advantages over conventional concrete, such as reducing labor and construction time, mainly because of its fluidity in the fresh state. However, in the hardened state, it maintains low performance when tensioned, and the fibers can be added to the mixture, maintaining a portion of the resistance after cracking. Steel fibers are usually added to concrete, but recently synthetic fibers have been used, due to their lower cost and non-corrosive nature, but with lower tensile strength. Thus, by combining the two types of fibers, the benefits of each material can be used. This work presents the results of an experimental program to evaluate the effect of the hybridization of metallic and synthetic fibers on the shear strength of self-compacting concrete beams without stirrups. The results demonstrate that both steel and hybrid fibers result in greater shear strength compared with the reference concrete without fibers before shear crack formation; however, the greatest advantages are attributed to post-cracking residual strength. The experimental results were compared with estimates calculated using equations published in the literature, demonstrating the feasibility of using some existing equations for concretes with the addition of hybrid fibers.
Keywords: self-compacting concrete, shear, synthetic fibers, concrete structures, beams
Introduction
Self-compacting concrete (SCC) is defined as a fresh concrete mixture that flows under its own weight without internal or external vibration. At the same time, this highly flowable mixture exhibits great cohesion, i.e., resistance to segregation between coarse aggregate and mortar, when flowing through reinforcing bars (Okamura & Ouchi, 2003). In this regard, the use of SCC reduces construction time and labor costs, leading to better working environments and more durable structures (Hossain et al., 2013).
Such fresh-state properties mainly depend on the cement paste microstructure density, which is modified by the incorporation of ultrafine particles and admixtures. Although SCC performs well in the fresh state, it behaves similarly to conventional concrete in the hardened state, i.e., as a brittle material with poor tensile strength.
Shear failure is an example of a tension-driven failure mode to which structural elements such as beams are often subjected (Torres & Lantsoght, 2019). Therefore, alternatives must be considered to enhance concrete material properties, such as fiber incorporation, which is a widely accepted technique. This approach improves not only tensile strength but also cracking behavior, toughness, ductility, flexural strength, impact strength, and fatigue resistance.
According to Rando et al., 2019, the addition of fibers does not aim to increase the concrete’s tensile strength; however, this can occur because the fibers restrain thermal fissure expansion. In addition, macro synthetic fibers have been shown to control shrinkage and thermal cracking in structural applications (Yazdanbakhsh et al., 2015).
In addition to steel and synthetic fibers, which are usually used for structural and non-structural purposes, respectively, a combination of both types is another option, called hybrid fibers. This allows combining the mechanical properties of different fiber types, taking advantage of the singular characteristics to achieve desirable behavior (Zhang et al., 2018), and changing the failure mode from shear to flexural (Torres & Lantsoght, 2019). The addition of hybrid fibers to concrete is also associated with delaying corrosion initiation and reducing the corrosion rate because of their resistance to crack propagation (Blunt et al., 2015).
Furthermore, the addition of fibers has improved the shear capacity of concrete beams, reducing the need for stirrups, and resulting in one of the most remarkable fiber applications in recent times (Lantsoght, 2019). The replacement of stirrups by steel fiber reinforcement is suggested to be a proportion of 0.6% and 1.2% of the fiber volume fraction of the cement mass according to Eurocode 2 (European, 2004) and ACI 318-14 (American, 2014), respectively. Moreover, Pauw et al., 2008 and Susetyo et al., 2011 showed that minimum shear reinforcement in beams could be replaced by the addition of steel addition to concrete, resulting in similar or even higher shear strength. In the first case, the failure load of beams with fiber addition was 2.6% greater than those beams reinforced with stirrups. For the second, a fiber volume content of 1.0% achieved satisfactory performance in terms of cracking behavior, deformation ductility, and shear strength.
Regardless of the concrete type, conventional or SCC, a significant improvement in the post-cracking behavior is observed when using hybrid fibers in beam manufacturing (Jen et al., 2016). Moreover, mono steel and hybrid fibers can enhance the ultimate bearing capacity of reinforced beams produced with self-compacting concrete. When fiber content is increased from 30 kg/m\(^3\) to 50 kg/m\(^3\), the longitudinal reinforcement crack width, crack spacing, and strain decrease significantly (Zhang et al., 2018).
To overcome the lack of mechanical models that accurately describe fiber-reinforced concrete behavior, empirical equations have been suggested throughout the years. Most equations only consider steel fibers as reinforcement, varying only the fiber factor. Laufer & Savaris, 2021 compared results from 113 self-compacting concrete beams with the addition of steel fibers using equations proposed to calculate the shear strength in conventional concrete beams with fibers. Although the code-based equations presented safer results, they are conservative, and some equations presented by the literature are not recommended for use in self-compacting concrete.
Therefore, this study aims to understand the influence of implementing both steel and hybrid steel polymeric macro fibers on the shear capacity of beams cast with self-compacting concrete and without shear reinforcement. Moreover, the literature models currently used to estimate the ultimate shear strength of steel fiber-reinforced concrete will be assessed and compared with the acquired experimental data.
Experimental procedure
Materials, mixtures, and specimens
A total of six beams (1000\(\times\)100\(\times\)200 mm) were molded with three self-compacting concrete mixtures following the recommendations of the European Federation for Specialist Construction Chemicals and Concrete Systems [EFNARC] (). Two types of fibers were used: corrugated steel fibers (SF) and synthetic polyethylene macrofibers (MF), as illustrated in Figures 1(a) and 1(b), the properties of which are given in Table 1.
| (a) | (b) |
 |  |
| Fiber | Composition | Length | Density | Tensile strength |
| (mm) | (g/cm\(^3\)) | (MPa) | ||
| SF | Steel | 40 | 7.85 | 800 |
| (I ASTM A 820) | ||||
| MF | Polyethylene | 50 | 1.12 | 350 |
| monofilaments |
From "Fibers for concrete" by MM fibers, .
The mix proportions are presented in Table 2, and the concrete components are as follows: Brazilian Portland cement type CP II-Z-32 (similar to ASTM Type IP), commonly used for structures; natural quartz-sand, with a fineness modulus of 1.51; basalt coarse aggregate with 9.5 mm maximum size; limestone filler; sodium polycarboxylate super-plasticizer (SP) TEC-FLOW 8000, used to adjust the flowability and cohesiveness of SCC (slump between 660 mm and 750 mm), and fiber addition: one mix without fiber addition (CR), one with 0.5% steel fibers (CFA) addition; and, one with hybrid fibers (0.25% steel fibers and 0.25% synthetic macro fibers) (CFH).
| Mistura | Cement | Sand | Filler | Gravel | Water | SP (g/m3) | SF | MF |
|---|---|---|---|---|---|---|---|---|
| CR | 360.00 | 824.00 | 184.00 | 734.33 | 208.67 | 360.00 | 0.00 | 0.00 |
| CFA | 360.00 | 824.00 | 184.00 | 734.33 | 208.67 | 360.00 | 40.00 | 0.00 |
| CFH | 360.00 | 824.00 | 184.00 | 734.33 | 208.67 | 360.00 | 20.00 | 2.80 |
The fiber content was limited to 0.5% for this work to avoid compromising the concrete workability, as per Torres and (Lantsoght, 2019), who recommended a maximum of 0.75% fiber addition. The evaluated mixtures resulted in concrete with compressive strength of approximately 30 MPa, water/cement ratio of 0.58, and superplasticizer content corresponding to 0.10% of the cement mass.
The first phase of the experiment was conducted to assess and validate the fresh and hardened state behavior of the concrete mixtures. Thirty liters of each mix was produced to adjust the superplasticizer content, targeting a flow-spread diameter without fibers of at least 700 mm. Figures 2(a)-2(c), show the slump flow tests performed for mixtures CR, CFA and CFH, respectively. In the second stage, fibers were gradually incorporated into the mixture to ensure that they were correctly dispersed. After five minutes of mixing, slump-flow, L-box, and funnel-V tests evaluated the mixture’s flowability, passing ability, and viscosity, respectively.
Finally, fifteen cylindrical specimens (10cm diameter and 20cm height) were molded for each mixture, demolded after 24 hours, and cured in water until 28 days of age.
Five specimens were tested for each mechanical property: axial compressive strength, modulus of elasticity, and splitting tensile strength, according to ASTM C469 (American Society for Testing & Materials, 2014).
| (a) | (b) | (c) |
 |  |  |
In the second concrete batch, 50 liters from each mixture was produced to mold two beams for shear strength tests, with the following dimensions: 100\(\times\)200\(\times\)1000 mm (width\(\times\)height\(\times\)length), and an effective depth (d) of 178.75 mm. Mechanical vibration was not used to fill the formwork. In addition, three cylindrical specimens were molded to evaluate the mixture’s axial compressive strength. After 24 hours, the beams were demolded, stored under canvas, moistened for seven days, and kept in ambient conditions until the test date of 28 days.
Beams were designed for shear failure, without stirrups. Two ribbed steel bars with a diameter of 12.5 mm (\(f_y=\)500 MPa) were used as longitudinal reinforcement, resulting in a reinforcement ratio (\(\rho\)) of 1.376%.
Steel bars CA60 with 5.0 mm diameter (\(f_y=\)600 MPa) were used as closed stirrups, placed in both extremities and the load application zone, to assist in correct reinforcement placement and avoid shear failure in these regions, as shown in Figure 3.
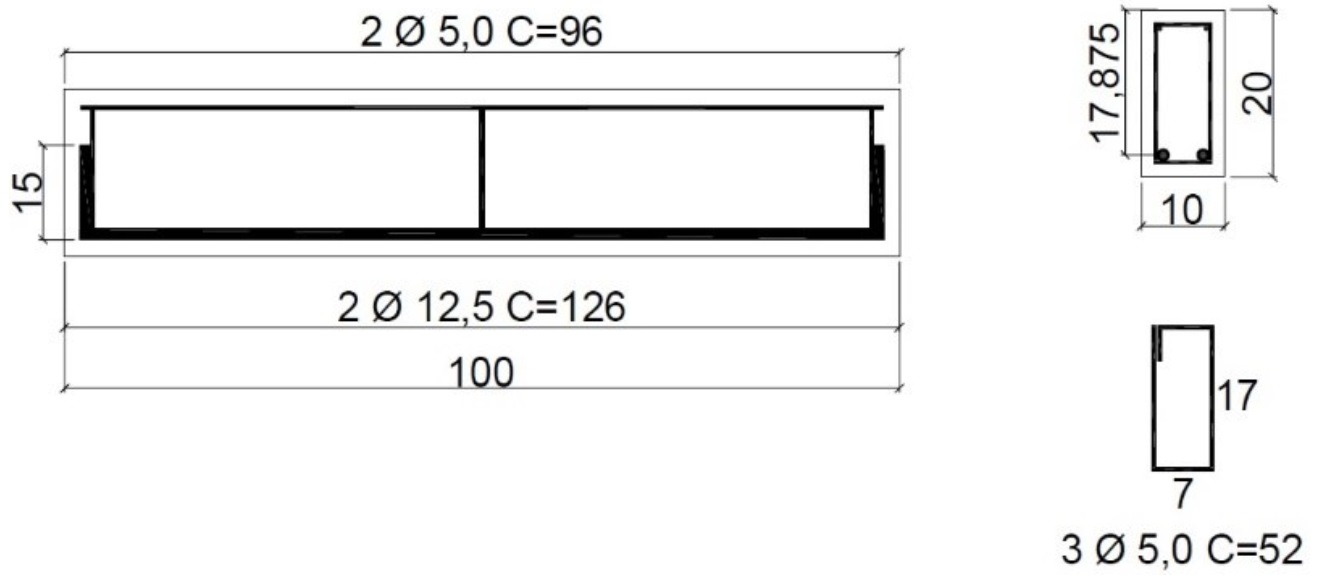 |
Testing procedure
The beam specimens were tested as simply supported beams under three-point loading condition, Figure 4. The test setup included a hydraulic jack with a load capacity of 500 kN that applied a load gradually on the mid-span of the beam specimens until shear failure was reached. Two linear variable displacement transducers (LVDTs) were attached, equally spaced from the loading point at 90° on the front surface of each beam, to measure the shear crack width. .
 |
Shear strength prediction equations
The experimental results of the ultimate shear strength are presented in Table [tab3], and were compared with theoretical models that predict the shear strength of fiber-reinforced concrete beams.
The actual models depend on the fiber factor (\(F\)), beam width (\(b\)), beam effective depth (\(d\)), the ratio between the shear span and the effective depth (\(a/d\)), maximum aggregate size (\(d_a\)), concrete compressive strength (\(f_c\)), concrete splitting tensile strength (\(f_{sp}\)), reinforcement ratio (\(\rho\)), and fiber bond (\(\tau\)) or resistance between the fiber and the concrete matrix.
Most empirical equations consider the fiber factor (\(F\)), calculated using equation (1), given by
\[ F = \frac{L_f}{D_f} \cdot V_f \cdot d_f,\]
defined by Singh, 2017 as a fiber property that depends on the fiber length \(L_f\) (mm), fiber diameter \(D_f\) (mm), fiber volume fraction \(V_f\) (%), and bond factor \(d_f\).
Narayanan & Darwish, 1987 recommended using bond factors of 0.5 for round fibers, 0.75 for crimped fibers, and 1.0 for indented fibers. When hybrid fibers are used, the \(F\) factor can be obtained by summing the \(F\) factors of each type of fiber placed in the system (Dev & Sabeena, 2018). Khuntia et al., 1999 recommended considering the fiber bond resistance (\(\tau\)) as \(0.66\sqrt{fc}\). Thus, the fiber factors (\(F\)) for the CFA and CFH mixtures were 0.0625 and 0.1250, respectively.
| Author | Proposed equation |
|---|---|
| Ashour et al. (1992) | \(V_u = \left[2.11\sqrt[3]{f_c} \left(\dfrac{\rho d}{a}\right)^{0.333}\right]bd\) for \(a/d \leq 2.5\) |
| Iman et al. (1997) | \(V_u = 0.6\psi\sqrt[3]{\omega} \left[f_c^{0.44} + 275\sqrt{\dfrac{\omega}{(a/d)^5}}\right]bd\) |
| \(\psi = \dfrac{1 + \sqrt{5.08/d_a}}{\sqrt{1 + 1/(25d_a)}}\) | |
| \(\omega = \rho(1 + 4F)\) | |
| Khuntia et al. (1999) | \(V_u = \left[(0.167 + 0.25F) \sqrt{f_c}\right]bd\) |
| Kwak et al. (2002) | \(V_u = \left[3.7e\left(\dfrac{f_{sp}}{a}\right)^{2/3}\left(\dfrac{\rho d}{a}\right)^{1/3} + {0.328}\tau_F\right]bd\) |
| \(e = \begin{cases} 3.4 \dfrac{d}{a}, & \text{for } a/d \leq 3.4 \\ 1, & \text{for } a/d > 3.4 \end{cases}\) | |
| Narayanan and Darwish (1987) | \(V_u = \left[e\left(0.24f_{sp} + 80\dfrac{\rho d}{a}\right) + 0.41{\tau_F}\right]bd\) |
| \(e = \begin{cases} 2.8 \dfrac{a}{d}, & \text{for } a/d \leq 2.8 \\ 1, & \text{for } a/d > 2.8 \end{cases}\) | |
| Sharma (1986) | \(V_u = \left[\frac{2}{3}f_{sp}\left(\dfrac{d}{a}\right)^{0.25}\right]bd\) |
Results
Fresh state properties
Through visual analysis, none of the mixtures evidenced segregation or exudation. Table 3 presents the fresh state behavior of the self-compacting concrete mixtures developed in this study. The slump flow was evaluated before and after fiber addition to investigate its influence on concrete flowability.
| Mixture | Slump-flow | Slump-flow | L-Box | V-Funnel |
| without fibers (mm) | with fibers (mm) | (s) | ||
| CR | 745.0 | - | 0.89 | 3.9 |
| CFA | 732.5 | 572.5 | 0.65 | 5.7 |
| CFH | 707.5 | 507.5 | 0.55 | 7.0 |
Before incorporating fibers in the mixtures, slump-flow was in the range of 660 to 750 mm, and is classified as SF2, according to EFNARC (), which is considered suitable for regular applications.
The fiber addiction significantly affected the concrete flowability, reducing by up to 20% and 30% of slump flow for CFA and CFH, respectively. Although, after incorporating the fibers, CFA is classified as SF1 (550-650 mm), which is appropriate for unreinforced or slightly reinforced concrete structures, CFH could no longer be classified as self-consolidating concrete. At this point, the authors highlight that the superplasticizer admixture could be added to CFH to obtain the requirement of at least 550 mm in the slump flow test; however, it was chosen to keep the same admixture amount for all mixtures. L-box test indicates the mixture passing ability, and according to the result should be at least 0.8, which was observed only for the CR mixture. In this case, it is notable that fibers considerably reduced the concrete passing ability, restraining concrete from flowing through the spaces between bars, as shown in Figure 5.
According to Ferrara et al., 2007, this test was developed based on common congested reinforcement patterns, and obstacle spacing is too narrow for the length of the fibers. For such cases, this parameter is not crucial when using fiber-reinforced self-compacting mixes.
According to EFNARC (), the time value obtained by the V-Funnel test describes the mixture flow rate, which is related to concrete viscosity, i.e., the lower the flow rate the higher the viscosity. As shown in Table 3, fiber addition increased the V-Funnel time, indicating higher viscosity and susceptibility to bleeding and segregation. However, all mixtures are classified as VF1 (V-funnel time less than 8 seconds) and have good filling ability and self-leveling.
 |
Hardened state properties
The compressive strength, splitting tensile strength and, modulus of elasticity of concrete specimens are summarized in Table 4. In general, fiber addition reduces the mechanical properties of concrete. There were 11.96% and 15.84% lower compressive strengths for CFA and CFH, respectively, compared with the reference concrete. Brown et al., 2010, attributed the reduction of compressive strength to the lack of consolidation, which was confirmed in this study by the reduction of slump flow when fibers were added to concrete. However, Tabatabaeian et al., 2017 considered the reduced compressive strength of concretes with polypropylene fibers to be due the increase in porosity and the rate of trapped air in the concrete.
The peak tensile strength was also lower for CFA and CFH than reference concrete by 5.90% and 15.50%, respectively. According to Fehling et al., 2014, concrete’s tensile strength is related to mortar strength, and only after the formation of the first crack the fibers work as bridges, transferring tension and generating ductility, however, this effect is affected by the dimensions, strength and amount of fibers added. Tabatabaeian et al., 2017 showed variation in the splitting tensile strength of concretes when using steel and polypropylene fibers, which they attributed to their different characteristics, such as length, shape, modulus of elasticity and tensile stress.
A one-way analysis of variance (ANOVA) was performed to statistically compare the differences between samples results, and determine whether fibers significantly affect the hardened state properties of the concrete. P-values were less than the significance level (0.05), indicating that not all mixture means are equal. Thus, the fibers affected the analyzed concrete properties considering the statistical difference scenarios. Moreover, Tukey-Kramer tests were performed to compare means, and values identified with the same letters indicate statistically equivalent means.
| Specimen | \(f_c\) | \(f_{t,sp}\) | \(E_c\) | ||||||||
| CR | CFA | CFH | CR | CFA | CFH | CR | CFA | CFH | |||
| 1 | 27.17 | 24.46 | 22.32 | 2.57 | 2.90 | 2.36 | 28.90 | 24.30 | 27.30 | ||
| 2 | 28.28 | 23.04 | 23.58 | 2.85 | 2.48 | 2.28 | 28.40 | 26.90 | 27.10 | ||
| 3 | 29.41 | 24.86 | 22.16 | 2.35 | 2.39 | 2.30 | 28.90 | 23.70 | 27.20 | ||
| 4 | 26.57 | 24.35 | 24.07 | 3.09 | 2.45 | 2.49 | 28.70 | 25.20 | 28.40 | ||
| 5 | 26.88 | 25.02 | 24.27 | 2.66 | 2.51 | 2.00 | 28.80 | 29.90 | 26.70 | ||
| Mean | 27.66a | 24.35b | 23.28b | 2.71a | 2.55ab | 2.29b | 28.74a | 26.00b | 27.34ab | ||
| Standard deviation | 1.17 | 0.78 | 0.98 | 0.28 | 0.20 | 0.18 | 0.21 | 2.49 | 0.63 | ||
| \(P\)-value | \(3.9 \times 10^{-5}\) | \(3.7 \times 10^{-2}\) | \(4.1 \times 10^{-2}\) | ||||||||
Values with the same letters indicate statistically equivalent means.
As a result, Table 4, the concrete mixture with hybrid fibers (CFH) presented similar compressive and tensile strengths similar to those of the mix with only steel fibers, but lower than the reference concrete. This indicates that the partial replacement of steel fibers with synthetic fibers is a viable alternative. However, the use of hybrid fibers did not affect the elastic modulus as did the steel fibers, presenting results similar to those of the refence concrete.
General cracking failure and behavior of the beams
The concretes produced for beam casting presented compressive strength measured by testing three cylindrical specimens molded similar to values from the first phase, with mean values equal to 24.78 MPa, 22.65 MPa, and 21.38 MPa, for CR, CFA, and CFH, respectively.
Figure 6 shows all beams after failure using the three-point bending test, and the indicated diagonal shear failure patterns. Because there was no shear reinforcement, shear crack formation occurred at mid-height and propagated to the load application and support points.
| (a) | (b) |
 |  |
| (c) | (d) |
 |  |
| (e) | (f) |
 |  |
The shear load-crack opening of each concrete mixture is presented in Figure 7. Beams cast with CR presented sudden failure after shear crack formation, whereas fiber-reinforced concrete beams presented post-cracking behavior with higher crack width.
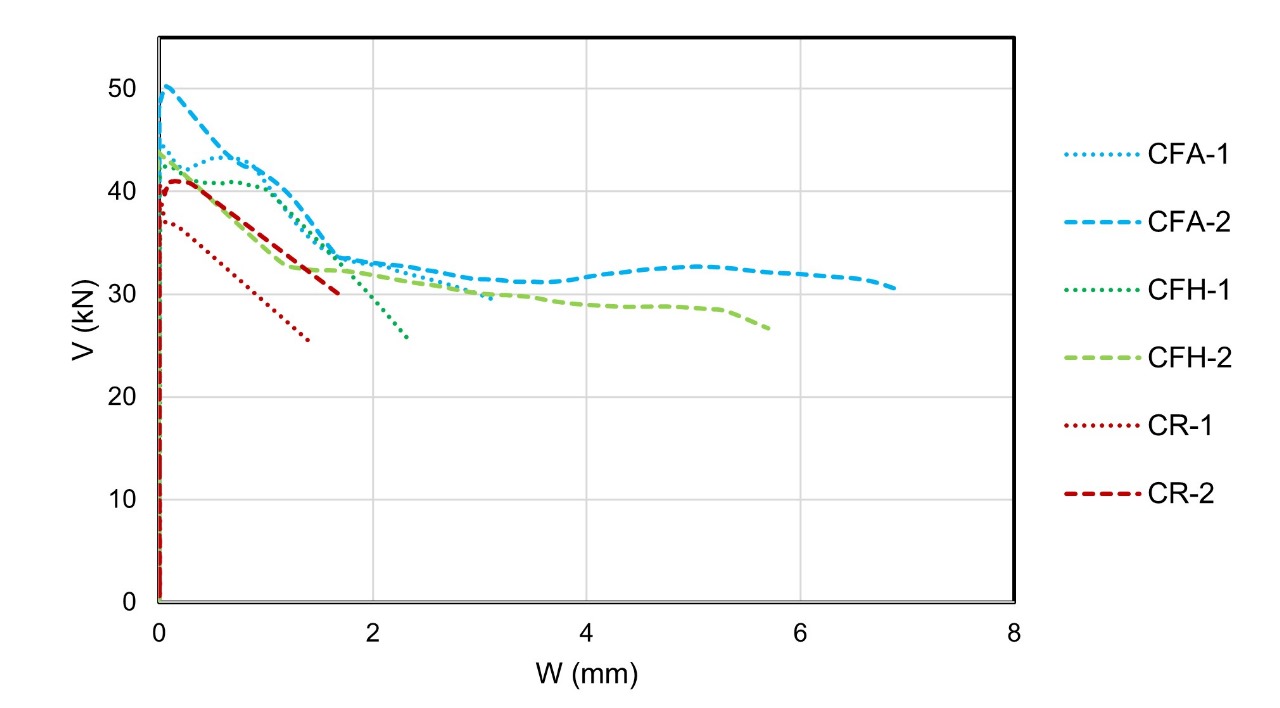 |
As the beam was loaded, the formation of diagonal cracks was visually observed, along with a sudden displacement measured by LVDTs on lateral surface of the beam. Table 5 presents the shear force at the first diagonal crack, crack inclination, the failure crack width, and the peak shear load of all beams. LVDTs were installed vertically, so the crack width was calculated considering the shear crack inclination, and values presented correspond to the perpendicular opening of the crack at the point intercepted by the LVDT.
| Mixture | Beam | Shear load (kN) | ||||
| At cracking | At failure | Crack inclination (\(^\circ\)) | Crack width | |||
| at failure (mm) | ||||||
| CR | 1 | 19.64 | 19.64 | 35 | 1.40 | |
| 2 | 18.35 | 20.50 | 29 | 1.76 | ||
| CFA | 1 | 18.42 | 22.30 | 34 | 3.17 | |
| 2 | 24.18 | 25.15 | 32 | 6.91 | ||
| CFH | 1 | 21.20 | 21.22 | 37 | 2.34 | |
| 2 | 20.35 | 21.93 | 36 | 5.70 | ||
The shear loads corresponding to diagonal crack formation were slightly higher for the CFA and CFH beams than for the CR beams; however, all beams had similar crack inclination values, ranging between 29° and 37°. The crack width at failure was greater for the beams containing fibers because of the fiber bridging effect, which enabled tension transfer through the cracks. Different inclination values can be explained by fiber dispersion and orientation, which cannot guarantee its homogeneity throughout the casting process. This effect is responsible for the higher ultimate shear loads in beams containing fibers. Singh & Jain, 2014 noted that fiber-reinforced concrete beams showed the widening of a prominent sloping crack, which anticipated an imminent collapse, and this behavior was also observed in the present work.
Figure 8 shows the load-deflection behavior of the beams and shows a similar flexural behavior among the beams; however, the fiber-reinforced concrete beams presented a slightly lower deflection. After the beginning of crack development, fibers increase the matrix strength, resulting in higher deflection at ultimate stress, similar to the results reported by Souza et al., 2018. The combination of steel and synthetic fibers, CFH, shows an intermediary behavior between CFA and CR, which may be related to the poor dispersion of fibers compared with CFA, similar to the results presented by Zhang et al., 2018.
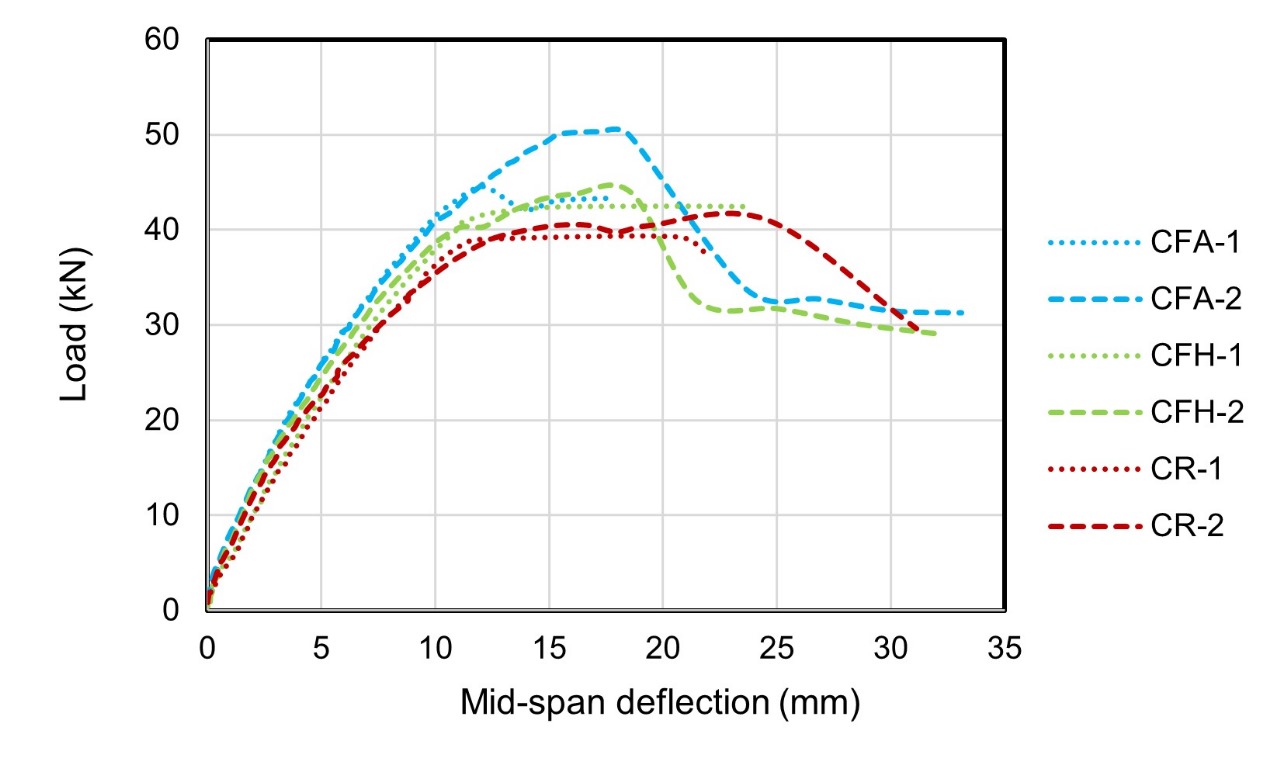
According to Rambo et al., 2014, the load-deflection curves can be divided into four main phases. In the first phase, an initial elastic response occurs, comprising a range between 0 mm and approximately 5 mm, which is practically unaltered by fiber presence, regardless of hybridization. The stretch between the beginning of load application and the maximum load resistance mainly refers to the elastic modulus of the composite, which depends on the characteristics of the cementitious matrix (Salvador & Figueiredo, 2013). Here we point out that the tested concretes presented similar elastic moduli, as seen in Table 5.
The proportionality limit delimits the second phase. It is observed that the reference concrete curves are below the fiber-reinforced concrete curves at this moment. The increased strength in the CFA and CFH beams is due to the bridging effect, which may connect the microcracks (Rambo et al., 2014). The third phase is characterized by hardening behavior, as evidenced by the appearance of a prominent crack. With crack widening, beam strength decreased, indicating the beginning of the fourth phase, which continues until the rupture.
Steel fiber addition showed the best behavior in the bending test, which achieved an average strength of 23.72 kN, representing an increase of 18% compared with the reference concrete. According to Salvador & Figueiredo, 2013, the post-cracking supported load increases with proportion of added fibers and depends on the fiber-concrete adherence and concrete elastic modulus. Thus, as expected, the post-cracking responses of the steel fiber reinforced concrete and hybrid fiber reinforced concrete differed. This behavior difference between the CFA and CFH curves upholds what was exposed by Salvador & Figueiredo, 2013 and by Kobayashi & Cho, 1982. Steel fiber reinforced concrete beams showed a strength decrease due to synthetic fiber slip as the load was transferred to them. Their energy-absorption capacity is recovered when the fiber anchorage is mobilized. For CFA-1, the residual strength increased by almost 14 mm to the mid-span deflection, and for CFA-2, it increased by up to 25 mm.
Regarding the curve’s behavior, when comparing fiber hybridization with the reference concrete, CFH-1 resulted in a 7.5% increase in the ultimate resisted load. It maintained greater resistance up to a 20 mm mid-span deflection, approximately. When comparing the bending test behavior and hardened state concrete properties, it was clear that fibers guarantee a more significant post-cracking behavior of self-consolidating concrete. Thus, despite the lower compressive strength resistance, the three-point bending test results confirm that fresh state properties do not influence the post-cracking behavior strength, as observed by Souza et al., 2018.
However, as the beam analysis was obtained using only two samples, it was not possible to perform statistical verification of the experimental results. Thus, to enable a statistical approval of the behavior of the studied beams, further studies will be conducted.
Beams shear strength prediction
The ultimate shear strength of fiber-reinforced beams estimated using equations is presented in Table [tab7] and compared with the values obtained experimentally.
| Model | Ultimate shear load (kN) | Vu\(_\text{exp}\) / Vu\(_\text{est}\) | |||
| CFA | CFH | CFA | CFH | ||
| Experimental (mean) | 23.72 | 21.58 | - | - | |
| Ashour et al. (1992) | 20.06 | 19.76 | 1.18 | 1.09 | |
| Iman et al. (1997) | 32.18 | 35.66 | 0.74 | 0.61 | |
| Khuntia et al. (1999) | 16.11 | 17.10 | 1.47 | 1.26 | |
| Kwak et al. (2002) | 35.56 | 34.32 | 0.67 | 0.63 | |
| Narayanan and Darwish (1987) | 26.18 | 26.21 | 0.91 | 0.82 | |
| Sharma (1986) | 24.85 | 22.31 | 0.95 | 0.97 | |
Equations proposed by Imam et al., 1997 and Kwak et al., 2002estimated the most discrepant results, where the estimated ultimate shear load differed more than 26% from the experimental results.
Besides its simplicity, the equation proposed by Sharma, 1986 yielded values of ultimate shear strength closest to the experimental results. This equation does not include any fiber parameter, and must be verified when a higher fiber ratio than that used in this study is employed.
Furthermore, it can be observed that the values estimated by equations that comprised the \(F\) factor were closer to those obtained experimentally for steel fiber-reinforced concrete beams, as expected. The equations that excluded the \(F\) factor, as proposed by Ashour et al., 1992 and Sharma, 1986, were more accurate to CFH. From these results, the importance of the use of the \(F\) factor to predict the shear strength could be questioned because the best prediction method, in this case, did not include this term.
Conclusions
This research evaluated the physical and mechanical properties of three self-compacting mixtures: reference without fibers, steel fiber-reinforced, and hybrid fiber-reinforced. The shear strength of beams without stirrups molded with the previously cited mixes was also analyzed.
Fiber addition significantly reduced the flowability of self-compacting concrete so that hybrid fiber-reinforced concrete could no longer be classified as self-compacting, suggesting that fiber addition to this type of concrete must be preceded by a mix design.
Results obtained for tensile and compressive strength were lower for fiber-reinforced concretes than for the reference concrete; however, fiber addition positively influenced concrete post-cracking behavior. Beams molded with concrete reinforced with fibers guarantee a higher shear strength. Furthermore, fiber addition ensured greater strength to the concrete before crack development and higher crack width values for ultimate load, indicating a better post-cracking behavior compared with the reference concrete. However, for such results to be statistically proven, using a more significant number of samples would be necessary.
The ultimate shear load values estimated using equations that considered the fiber factor were closer to the results obtained experimentally for steel fiber reinforced concrete, justifying the need for studies that comprise hybrid fiber reinforcement for establishing improved equations.
Author contributions
I.E. da Silva participated in: Conceptualization, Data Curation, Formal Analysis, Methodology, Investigation, Resources, Visualization, Writing (preparation of the original draft). I.G. Laufer and A.C. Bergmann participated in: Conceptualization, Formal Analysis, Writing (revision and editing). G. Savaris participated in: Conceptualization, Data Curation, Formal Analysis, Methodology, Project Managements, Resources, Supervision, Writing (revision and editing). R.J.M Fakhye participated in: Methodology, Formal Analysis, Writing (revision and editing). C.E.T. Balestra participated in: Resources, Formal Analysis, Writing (revision and editing).
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgments
The authors gratefully acknowledge the Federal University of Technology – Paraná, MM Fibras®, GCP Applied Technologies, and Materials and Structures Research Group (GPMAES) for their support in developing this research.
References
American Concrete Institute (2014). Committee 318: Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary (ACI 318R-14). American Concrete Institute.
American Society for Testing & Materials (2014). ASTM Standard C469/C469M-14 Standard Test Method for Static Modulus of Elasticity and Poisson's Ratio of Concrete in Compression. ASTM International.
Ashour, S. A., Hasanain, G. S. & Wafa, F. F. (1992). Shear Behavior of High-Strength Fiber Reinforced Concrete Beams. ACI Structural Journal, 89, 176–184. https://doi.org/10.14359/2946
Blunt, J., Jen, G. & Ostertag, C. P. (2015). Enhancing corrosion resistance of reinforced concrete structures with hybrid fiber reinforced concrete. Corrosion Science, 92, 182–191. https://doi.org/10.1016/j.corsci.2014.12.003
Brown, M. C., Ozyildirim, H. C. & Duke, W. L. (2010). Investigation of Steel and Polymer Fiber Reinforced Self-Consolidating Concrete. In C. M. Aldea & L. Ferrara (Eds.), Sp 274: Fiber reinforced self-consolidating concrete: Research and applications.
Dev, A. & Sabeena, M. V. (2018). Mechanical Properties of Hybrid Fiber Reinforced Concrete. 5(4), 2164-2168.
European Committee for Standardization (2004). EN 1992-1-1: Eurocode 2: Design of Concrete Structures: Part 1-1-General Rules and Rules for Buildings.
European Federation of Specialist Construction Chemicals & Concrete Systems (2002). Specification and Guidelines for Self-Compacting Concrete.
European Federation for Specialist Construction Chemicals & Concrete Systems (2005). The European Guidelines for Self-Compacting Concrete Specification, Production and Use.
Fehling, E., Schmidt, M., Walraven, J., Leutbecher, T. & Fröhlich, S. (2014). Ultra-High Performance Concrete UHPC: Fundamentals, Design, Examples. Wilhelm Ernst & Sohn.
Hossain, K. M. A., Lachemi, M., Sammour, M. & Sonebi, M. (2013). Strength and fracture energy characteristics of self-consolidating concrete incorporating polyvinyl alcohol, steel and hybrid fibres. 20-29. https://doi.org/10.1016/j.conbuildmat.2013.03.054
Imam, M., Vandewalle, L., Mortelmans, F. & van Gemert, D. (1997). Shear domain of fiber-reinforced high-strength concrete beams. 19(9), 738-747. https://doi.org/10.1016/S0141-0296(96)00150-2
Jen, G., Trono, W. & Ostertag, C. P. (2016). Self-consolidating hybrid fiber reinforced concrete: Development, properties and composite behavior. Construction and Building Materials, 104, 63–71 https://doi.org/10.1016/j.conbuildmat.2015.12.062
Khuntia, M., Stojakinovic, B. & Goel, S. (1999). Shear Strength of Normal and High-Strength Fiber Reinforced Concrete Beams without Stirrups. 282-289. https://doi.org/10.14359/620
Kobayashi, K. & Cho, R. (1982). Flexural characteristics of steel fiber and polyethylene fiber hybrid-reinforced concrete. 164-168. https://doi.org/10.1016/0010-4361(82)90054-4
Kwak, Y., Eberhard, M. O., Kim, W. & Kim, J. (2002). Shear Strength of Steel Fiber Reinforced Concrete Beams without Stirrups. 530-538. https://doi.org/10.14359/12122
Lantsoght, E. O. L. (2019). Database of shear experiments on steel fiber reinforced concrete beams without stirrups. 16(6), 917. https://doi.org/10.3390/ma12060917
Laufer, I. de G. & Savaris, G. (2021). Shear strength of steel fiber self-compacting concrete beams. 42(1), 45-62. https://doi.org/10.5433/1679-0375.2021v42n1p45
MM Fibers (2023). Fibers for concrete.
Narayanan, R. & Darwish, I. Y. S. (1987). Use of Steel Fibers as Shear Reinforcement. 84(3), 216--227. https://doi.org/10.14359/2654
Okamura, H. & Ouchi, M. (2003). Self-Compacting Concrete. 1(1), 5--15.
Rambo, D. A. S., Silva, F. D. A. & Toledo Filho, R. D. (2014). Effect of steel fiber hybridization on the fracture behavior of self-consolidating concretes. 100--109. https://doi.org/10.1016/j.cemconcomp.2014.02.004
Rando, A. M., Jr., Guerra, L. & Morales, G. (2019). Interference from the addition of polypropylene fibers and thin basalt on mechanical strength of micro concrete. 40(1), 55--62. https://doi.org/10.5433/1679-0375.2019v40n1p55
Salvador, R. P. & Figueiredo, A. D. (2013). Análise comparativa de comportamento mecânico de concreto reforçado com macrofibra polimérica e com fibra de aço. 1273--1285. https://doi.org/10.1590/S1517-70762013000200003
Sharma, A. K. (1986). Shear strength of steel fiber reinforced concrete beams. 624--628. https://doi.org/10.14359/10559
Singh, B. & Jain, K. (2014). Appraisal of Steel Fibers as Minimum Shear Reinforcement in Concrete Beams. 111(5), 1191--1202. https://doi.org/10.14359/51686969
Singh, H. (2017). Steel Fiber Reinforced Concrete. Springer Singapore. https://doi.org/10.1007/978-981-10-2507-5
Souza, D. A., Melo, A. H. V., DIAS, G. S., Vasconcelos, C. V. S. A. & Barboza, A. S. R. (2018). Avaliação do comportamento no pós fissuração de concreto com reforço híbrido de fibras. In Instituto Brasileiro do Concreto, 60º Congresso Brasileiro do Concreto.
Susetyo, J., Gauvreau, P. & Vecchio, F. J. (2011). Effectiveness of Steel Fiber as Minimum Shear Reinforcement. 108(4), https://doi.org/10.14359/51682990
Tabatabaeian, M., Khaloo, A., Joshaghani, A. & Hajibandeh, E. (2017). Experimental investigation on effects of hybrid fibers on rheological, mechanical, and durability properties of high-strength SCC. 497--509. https://doi.org/10.1016/j.conbuildmat.2017.04.181
Torres, J. A. & Lantsoght, E. O. L. (2019). Influence of Fiber Content on Shear Capacity of Steel Fiber-Reinforced Concrete Beams. 7(12), 102. https://doi.org/10.3390/fib7120102
Yazdanbakhsh, A., Altoubat, S. & Rieder, K. A. (2015). Analytical study on shear strength of macro synthetic fiber reinforced concrete beams. 622--632. https://doi.org/10.1016/j.engstruct.2015.06.034
Zhang, C., Han, S. & Hua, Y. (2018). Flexural performance of reinforced self-consolidating concrete beams containing hybrid fibers. 11--23. https://doi.org/10.1016/j.conbuildmat.2018.04.075
